Level Order Binary Traversal:
breadth-first traversal
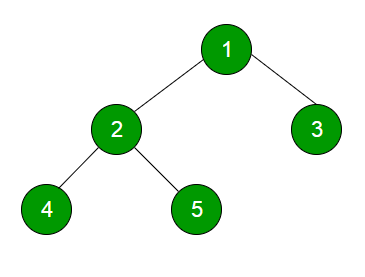
Level order traversal of the above tree is 1 2 3 4 5
Iterative:
void printLevelOrder(Node *root)
{
// Base Case
if (root == NULL) return;
// Create an empty queue for level order traversal
queue<Node *> q;
// Enqueue Root and initialize height
q.push(root);
while (q.empty() == false)
{
// Print front of queue and remove it from queue
Node *node = q.front();
cout << node->data << " ";
q.pop();
/* Enqueue left child */
if (node->left != NULL)
q.push(node->left);
/*Enqueue right child */
if (node->right != NULL)
q.push(node->right);
}
}
Reverse Level Order Traversal
Reverse Level order traversal of the above tree is “4 5 2 3 1”.
vector<int> reverseLevelOrder(Node *root)
{
vector<int> v;
queue<Node*> q;
q.push(root);
while(!q.empty()){
Node* front=q.front();
v.push_back(front->data);
q.pop();
//Attention: Right subtree is visited before left subtree
if(front->right) q.push(front->right);
if(front->left) q.push(front->left);
}
// or can use stack, then do not need to reverse
reverse(v.begin(),v.end());
return v;
}
height of Binary Tree:
int height(struct Node* node)
{ //base case
if(!node) return 0;
/* compute the depth of each subtree */
int leftH=height(node->left);
int rightH=height(node->right);
// choose max depth
if(leftH>rightH) return 1+leftH;
else return 1+rightH;
}
Diameter of Binary Tree:
The diameter of a tree is the number of nodes on the longest path between two leaves in the tree
// helper function
int height(Node* root, int& ans)
{
if (root == NULL)
return 0;
int leftH = height(root->left, ans);
int rightH = height(root->right, ans);
// update the answer, because diameter of a
// tree is nothing but maximum value of
// (left_height + right_height + 1) for each node
ans = max(ans, 1 + leftH + rightH);
// it return height of node
return 1 + max(leftH, rightH);
}
// Function to return the diameter of a Binary Tree.
int diameter(struct Node* root) {
if(!root) return 0;
int ans = INT_MIN; // This will store the final answer
height(root, ans);
return ans;
}
gfg Determine if Two Trees are Identical
//Function to check if two trees are identical.
bool isIdentical(Node *node1, Node *node2)
{
//both node not exist
if(!node1 && !node2) return true;
//if node exist, identical when three condition satisfied
Note: we also can remove else if -> if and last else ->______like in isMirror
function below
else if(node1&&node2){
return (
(node1->data==node2->data)
&&isIdentical(node1->left,node2->left)
&& isIdentical(node1->right,node2->right)
);
}
// one of them node not exist
else{
return false;
}
}
Making Mirror Tree:
void mirror(Node* root) {
if(!root) return;
queue<Node*> q;
q.push(root);
// Do BFS. While doing BFS, keep swapping
// left and right children
while(!q.empty()){
Node* node=q.front();
q.pop();
// swap left child with right child
swap(node->left,node->right);
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
}
check two tree are Mirror image of Each Other or not:
bool isMirror(struct Node* root1,struct Node* root2){
if(!root1 && !root2) return true;
// For two trees to be mirror
// images, the following
// three conditions must be true
// 1 - Their root node's
// key must be same 2 - left
// subtree of left tree and right subtree
// of right tree have to be mirror images
// 3 - right subtree of left tree and left subtree
// of right tree have to be mirror images
above comment saying there is one diffrence b/w isIdentical and isMirror image
see both code condition
if(root1&&root2){
return(
(root1->data==root2->data) &&
isMirror(root1->left,root2->right)&&
isMirror(root1->right, root2->left)
);
}
//else if, one of them root not exist
return false;
}
Symmetric Tree
binary tree is a Mirror image of itself
For example, this binary tree is symmetric:
1
/ \
2 2
/ \ / \
3 4 4 3 But the following is not:
1
/ \
2 2
\ \
3 3
Trick in coding: make helper function, check isMirror or not
Lekin isMirror to do root leta hai argument me, to bhai hum dono me
same root bhej denge
gfg check Symmteric Tree or not
bool isSymmetric(struct Node* root)
{
return isMirror(root,root);
}
//helper function
int height(Node* root){
if(!root) return 0;
int leftH=height(root->left);
int rightH=height(root->right);
return 1+max(leftH,rightH);
}
//Function to check whether a binary tree is balanced or not.
bool isBalanced(Node *root)
{
// if tree is empty
if(!root) return true;
// height of left and right subtree
int lH=height(root->left);
int rH=height(root->right);
bool cond1= abs(lH-rH)<=1;
bool cond2= isBalanced(root->left) && isBalanced(root->right);
if(cond1 && cond2) return true;
return false;
}
int getData(Node* node){
if(!node) return 0;
return node->data;
}
//Function to check whether all nodes of a tree have the value
//equal to the sum of their child nodes.
int isSumProperty(Node *root)
{
if(!root) return 1;
// using bfs
queue<Node*> q;
q.push(root);
while(!q.empty()){
Node* node=q.front();
q.pop();
bool cond1=getData(node)!=(getData(node->left)+getData(node->right));
// node must not leaf node
bool cond2= node->left || node->right;
if(cond1 && cond2) return 0;
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
return 1;
}
Check Binary Tree is BST or Not:
// helper function , BST helper function
bool isBSTH(Node* node,int min,int max){
if(!node) return true;
// no duplicate allowed => we use = for false cond
if(node->data<= min || node->data>=max) return false;
return (isBSTH(node->left,min,node->data) &&
isBSTH(node->right,node->data,max)
);
}
//Function to check whether a Binary Tree is BST or not.
bool isBST(Node* root)
{
return isBSTH(root,INT_MIN,INT_MAX);
}
sorted Array to BST:
vector<double> v;
vector<double> averageOfLevels(TreeNode* root) {
queue<TreeNode*> q;
q.push(root);
while(!q.empty()){
int n=q.size(); // size of q
double sum=0;
for(int i=0;i<n;i++){
TreeNode* frontNode=q.front();
sum+=frontNode->val;
q.pop();
if(frontNode->left) q.push(frontNode->left); // if left child add to queue
if(frontNode->right) q.push(frontNode->right); // if right child add to queue
}
double avg=sum/n;
v.push_back(avg);
}
return v;
}
vector<int> largestValues(Node* root)
{
vector<int> v;
if(!root) return v;
queue<Node*> q;
q.push(root);
while(!q.empty()){
int n=q.size();
int maxx=INT_MIN;
for(int i=0;i<n;i++){
Node* frontNode=q.front();
q.pop();
maxx=max(maxx,frontNode->data);
if(frontNode->left) q.push(frontNode->left);
if(frontNode->right) q.push(frontNode->right);
}
v.push_back(maxx);
}
return v;
}
void BST(vector<int>& nums,int l,int r,vector<int> &bstV){
if(l>r) return;
int mid=(l+r)/2;
bstV.push_back(nums[mid]);
BST(nums,l,mid-1,bstV);
BST(nums,mid+1,r,bstV);
}
vector<int> sortedArrayToBST(vector<int>& nums) {
vector<int> bstV;
BST(nums,0,nums.size()-1,bstV);
return bstV;
}
vector <int> zigZagTraversal(Node* root)
{
vector<int> v;
if(!root) return v;
queue<Node*> q;
q.push(root);
int level=0;
while(!q.empty()){
int n=q.size();
vector<int> tmp;
for(int i=0;i<n;i++){
Node* frontNode=q.front();
q.pop();
//odd level
if(level & 1) tmp.push_back(frontNode->data);
else v.push_back(frontNode->data);
if(frontNode->left) q.push(frontNode->left);
if(frontNode->right) q.push(frontNode->right);
}
if(level & 1) reverse(tmp.begin(),tmp.end());
for(auto x: tmp) v.push_back(x);
level++;
}
return v;
}
Searching a Key in BST:
// C function to search a given key in a given BST
struct node* search(struct node* root, int key)
{
// Base Cases: root is null or key is present at root
if (root == NULL || root->key == key)
return root;
// Key is greater than root's key
if ( key > root->key)
return search(root->right, key);
// Key is smaller than root's key
return search(root->left, key);
}
iterative searching:
// Function to check the given key exist or not
bool iterativeSearch(struct Node* root, int key)
{
// Traverse until root reaches to dead end
while (root != NULL) {
// pass right subtree as new tree
if (key > root->data)
root = root->right;
// pass left subtree as new tree
else if (key < root->data)
root = root->left;
else
return true; // if the key is found return 1
}
return false;
}
Insertion of Key in BST:
There must be no duplicate nodes.
A new key is always inserted at the leaf. We start searching a key from the root until we hit a leaf node. Once a leaf node is found, the new node is added as a child of the leaf node.
100 100
/ \ Insert 40 / \
20 500 ---------> 20 500
/ \ / \
10 30 10 30
\
40// C++ program to demonstrate insertion
// in a BST recursively.
#include <iostream>
using namespace std;
class BST
{
int data;
BST *left, *right;
public:
// Default constructor.
BST();
// Parameterized constructor.
BST(int);
// Insert function.
BST* Insert(BST*, int);
// Inorder traversal.
void Inorder(BST*);
};
// Default Constructor definition.
BST ::BST()
: data(0)
, left(NULL)
, right(NULL)
{
}
// Parameterized Constructor definition.
BST ::BST(int value)
{
data = value;
left = right = NULL;
}
// Insert function definition.
BST* BST ::Insert(BST* root, int value)
{
if (!root)
{
// Insert the first node, if root is NULL.
return new BST(value);
}
// Insert data.
if (value > root->data)
{
// Insert right node data, if the 'value'
// to be inserted is greater than 'root' node data.
// Process right nodes.
root->right = Insert(root->right, value);
}
else
{
// Insert left node data, if the 'value'
// to be inserted is greater than 'root' node data.
// Process left nodes.
root->left = Insert(root->left, value);
}
// Return 'root' node, after insertion.
return root;
}
// Inorder traversal function.
// This gives data in sorted order.
void BST ::Inorder(BST* root)
{
if (!root) {
return;
}
Inorder(root->left);
cout << root->data << endl;
Inorder(root->right);
}
// Driver code
int main()
{
BST b, *root = NULL;
root = b.Insert(root, 50);
b.Insert(root, 30);
b.Insert(root, 20);
b.Insert(root, 40);
b.Insert(root, 70);
b.Insert(root, 60);
b.Insert(root, 80);
b.Inorder(root);
return 0;
}
Note: inorder of BST gives sorted order
reference: https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-insertion/
Inorder successor in BST:
uss node ke right me minimum value
/* Given a non-empty binary search tree, return the node
with minimum key value found in that tree. Note that the
entire tree does not need to be searched. */
struct node* minValueNode(struct node* node)
{
struct node* current = node;
/* loop down to find the leftmost leaf */
while (current && current->left != NULL)
current = current->left;
return current;
}
// node with two children: Get the inorder successor
// (smallest in the right subtree)
struct node* temp = minValueNode(root->right);
Deletion in BST:
When we delete a node, three possibilities arise.
1) Node to be deleted is the leaf: Simply remove from the tree.
50 50
/ \ delete(20) / \
30 70 ---------> 30 70
/ \ / \ \ / \
20 40 60 80 40 60 802) Node to be deleted has only one child: Copy the child to the node and delete the child
50 50
/ \ delete(30) / \
30 70 ---------> 40 70
\ / \ / \
40 60 80 60 803) Node to be deleted has two children: Find inorder successor of the node. Copy contents of the inorder successor to the node and delete the inorder successor. Note that inorder predecessor can also be used.
50 60
/ \ delete(50) / \
40 70 ---------> 40 70
/ \ \
60 80 80The important thing to note is, inorder successor is needed only when the right child is not empty. In this particular case, inorder successor can be obtained by finding the minimum value in the right child of the node.
struct node* deleteNode(struct node* root, int key)
{
// base case
if (root == NULL)
return root;
// If the key to be deleted is
// smaller than the root's
// key, then it lies in left subtree
if (key < root->key)
root->left = deleteNode(root->left, key);
// If the key to be deleted is
// greater than the root's
// key, then it lies in right subtree
else if (key > root->key)
root->right = deleteNode(root->right, key);
// if key is same as root's key, then This is the node
// to be deleted
else {
// node has no child, leaf node simply delete(link tod di parent se)
// parent ke left ya right me NULL store ho jayega see above if else if
if (root->left==NULL and root->right==NULL)
return NULL;
// node with only one child or no child
else if (root->left == NULL) {
struct node* temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL) {
struct node* temp = root->left;
free(root);
return temp;
}
// node with two children: Get the inorder successor
// (smallest in the right subtree)
struct node* temp = minValueNode(root->right);
// Copy the inorder successor's content to this node
// mtlb jisko delete krna tha uski value badal di bs
//aur ab succeccesor ko delete krna padega, usko delete
// krne ke liye fir sare cases dekhne padenge
root->key = temp->key;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->key);
}
return root;
}
Find the node with minimum value in a Binary Search Tree:
// Note that the entire tree does not need
// to be searched.
int minValue(struct node* node)
{
struct node* current = node;
/* loop down to find the leftmost leaf */
while (current->left != NULL)
{
current = current->left;
}
return(current->data);
}
Find the node with maximum value in a Binary Search Tree:
Like Above: we can get the maximum value by recursively traversing the right node of a binary search tree.
as we know: inorder traversal is: left root right
so,reverse inorder traversal : right root left
inorder of BST gives: sorted increasing order
reverse inorder of BST will give: sorted decreasing order
Application of reverse inorder:
Find K’th Largest Element in BST
void kthLargestUtil(Node *root, int k, int &c)
{
// Base cases, the second condition is important to
// avoid unnecessary recursive calls
if (root == NULL || c >= k)
return;
// Follow reverse inorder traversal so that the
// largest element is visited first
kthLargestUtil(root->right, k, c);
// Increment count of visited nodes
c++;
// If c becomes k now, then this is the k'th largest
if (c == k)
{
cout << "K'th largest element is "
<< root->key << endl;
return;
}
// Recur for left subtree
kthLargestUtil(root->left, k, c);
}
// Function to find k'th largest element
void kthLargest(Node *root, int k)
{
// Initialize count of nodes visited as 0
int c = 0;
// Note that c is passed by reference
kthLargestUtil(root, k, c);
}
as we know: 1 2 4 is subsequence of 1234
1 2 4 is not subarray/substring of 1234
A subset is any possible combination of the original set. The term subset is often used for subsequence,but that's not
right. A subsequence always maintains the
relative order
of the
array elements (i.e., increasing index), but there
is no such restriction on a subset. For example, { 3,
1} is a valid subset of { 1, 2, 3
, 4,
5 }
, but
it is neither a subsequence nor a subarray.
Check if given sorted sub-sequence exists in binary search tree:
using inorder fashion:
// function to check if given sorted sub-sequence exist in BST
// index --> iterator for given sorted sub-sequence
// seq[] --> given sorted sub-sequence
void seqExistUtil(struct Node *ptr, int seq[], int &index)
{
if (ptr == NULL)
return;
// We traverse left subtree first in Inorder
seqExistUtil(ptr->left, seq, index);
// If current node matches with se[index] then move
// forward in sub-sequence
if (ptr->data == seq[index])
index++;
// We traverse left subtree in the end in Inorder
seqExistUtil(ptr->right, seq, index);
}
// A wrapper over seqExistUtil. It returns true
// if seq[0..n-1] exists in tree.
bool seqExist(struct Node *root, int seq[], int n)
{
// Initialize index in seq[]
int index = 0;
// Do an inorder traversal and find if all
// elements of seq[] were present
seqExistUtil(root, seq, index);
// index would become n if all elements of
// seq[] were present
return (index == n);
}
Print BST keys in the given range:
/* The functions prints all the keys
which in the given range [k1..k2].
The function assumes than k1 < k2 */
void Print(node *root, int k1, int k2)
{
/* base case */
if ( NULL == root )
return;
/* Since the desired o/p is sorted,
recurse for left subtree first
If root->data is greater than k1,
then only we can get o/p keys
in left subtree */
if ( k1 < root->data )
Print(root->left, k1, k2);
/* if root's data lies in range,
then prints root's data */
if ( k1 <= root->data && k2 >= root->data )
cout<<root->data<<" ";
/* recursively call the right subtree */
Print(root->right, k1, k2);
}
Remove all leaf nodes from the BST:
// Delete leaf nodes from binary search tree.
struct Node* leafDelete(struct Node* root)
{
if (root == NULL)
return NULL;
if (root->left == NULL && root->right == NULL) {
free(root);
return NULL;
}
// Else recursively delete in left and right
// subtrees.
root->left = leafDelete(root->left);
root->right = leafDelete(root->right);
return root;
}
------------------------------------------------------




Comments
Post a Comment